Index
- Guessing Game
- Common Programming Concepts
- Understanding Ownership
- Using Structs
- Enums and Pattern Matching
- Managing Growing Projects with Packages, Crates, and Modules
- Defining Modules to Control Scope and Privacy
- Paths for Referring to an Item in the Module Tree
- Bringing Paths into Scope with the use Keyword
- Separating Modules into Different Files
- Common Collections
- Error Handling
- Generic Types, Traits, and Lifetimes
- Writing Automated Tests
- Object Oriented Programming
- Adding dependancies
- Option Take
- RefCell
- mem
- Data Structure
- Recipe
- Semi colon
- Calling rust from python
- Default
- Crytocurrency With rust
- Function chaining
- Question Mark Operator
- Tests with println
- lib and bin
- Append vector to hash map
- Random Number
- uuid4
- uwrap and option
- Blockchain with Rust
- Near Protocol
- Actix-web
Binary search tree
Code:
https://github.com/PacktPublishing/Hands-On-Data-Structures-and-Algorithms-with-Rust/blob/master/Chapter05/src/binary_search_tree.rs
Data structures: Binary Search Tree
https://www.youtube.com/watch?v=pYT9F8_LFTM
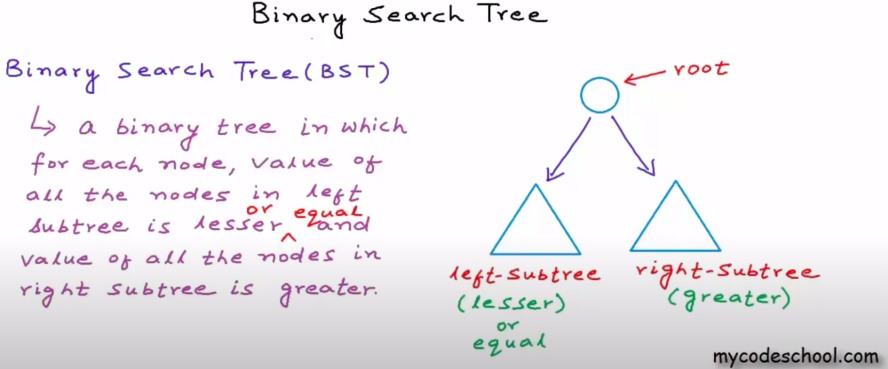
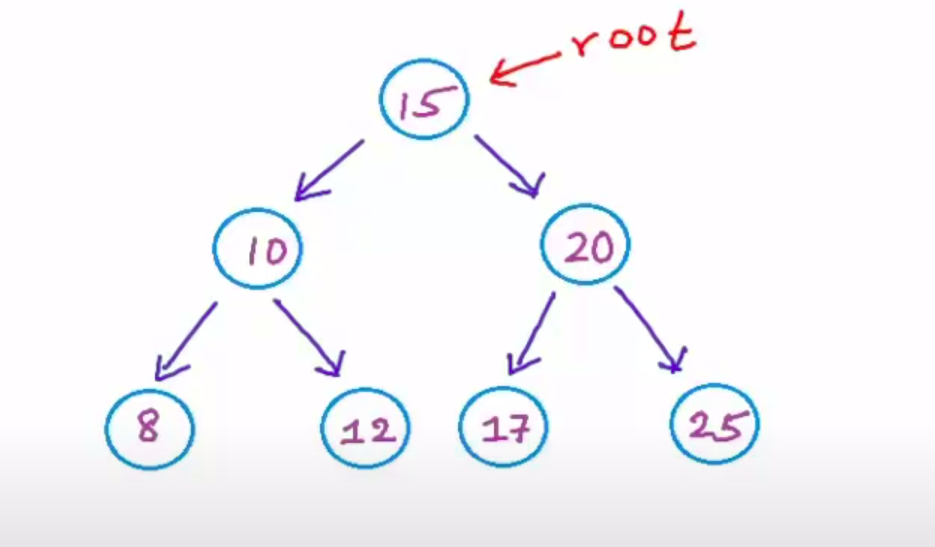
A tree structure is almost like a linked list: each node has branches—in the case of a binary tree, there are two—which represent children of that node. Since these children have children of their own, the node count grows exponentially, building a hierarchical structure that looks like a regular tree turned on its head.
Binary trees are a subset of these structures with only two branches, typically called left and right.
However, that does not inherently help the tree's performance. This is why using a binary search tree, where left represents the smaller or equal value to its parent, and right anything that's greater than that parent node, was established!
If that was confusing, don't worry; there will be code. First, some vocabulary though: what would you call the far ends of the tree? Leaves. Cutting off branches? Pruning. The number of branches per node? Branching factor (binary trees have a branching factor of 2)
fn main() {
type Tree = Option<Box<Node>>;
struct Node {
pub value: u64,
left: Tree,
right: Tree,
}
// 1. Tree structure itself is only a pointer to the root node
pub struct BinarySearchTree {
root: Tree,
pub length: u64,
}
}
type Tree = Option<Box<Node>>;
struct Node {
pub value: u64,
left: Tree,
right: Tree,
}
// 1. Tree structure itself is only a pointer to the root node
pub struct BinarySearchTree {
root: Tree,
pub length: u64,
}
}
Store IoT device objects (containing the IP address, numerical name, and type)
Retrieve IoT objects by numerical name
Iterate over IoT objects
A great use for a tree: the numerical name can be used to create a tree and search for it nice and quickly.
#[derive(Clone, Debug)]
pub struct IoTDevice {
pub numerical_id: u64,
pub address: String,
}
pub struct IoTDevice {
pub numerical_id: u64,
pub address: String,
}
For simplicity, this object will be used in the code directly (adding generics isn't too tricky, but would go beyond the scope of this book):
type Tree = Option<Box<Node>>;
struct Node {
pub dev: IoTDevice,
left: Tree,
right: Tree,
}
struct Node {
pub dev: IoTDevice,
left: Tree,
right: Tree,
}
Starting with this basic implementation, the requisite operations, add and find, can be implemented.
More devices
Unlike lists, trees make a major decision on insert: which side does the new element go to? Starting at the root node, each node's value is compared to the value that is going to be inserted: is this greater than or less than that? Either decision will lead down a different subtree (left or right).
This process is (usually recursively) repeated until the targeted subtree is None, which is exactly where the new value is inserted—as a leaf of the tree. If this is the first value going into the tree, it becomes the root node. There are some problems with this, and the more experienced programmers will have had a strange feeling already: what happens if you insert numbers in ascending order?
These feelings are justified. Inserting in ascending order (for example, 1, 2, 3, 4) will lead to a tree that is basically a list in disguise! This is also called a (very) unbalanced tree and won't have any of the benefits of other trees:
1
/ \
2
/ \
3
/ \
4
During this chapter, we are going to go a lot more things on balancing trees and why that is important in order to achieve high performance. In order to avoid this pitfall associated with binary search trees, the first value to insert should ideally be the median of all elements since it will be used as the root node, as is visible in the following code snippet:
Insert some record:
https://youtu.be/pYT9F8_LFTM?t=1065
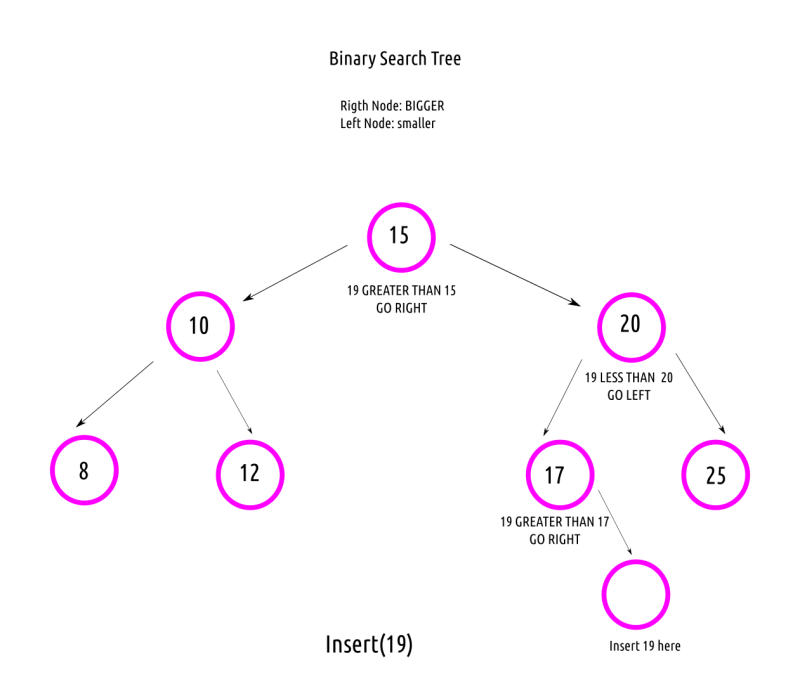
Remember we can also reverse it turning left to right, and the algorithm will not change.
use std::mem;
fn main() {
type Tree = Option<Box<Node>>;
#[derive(Clone, Debug)]
pub struct IoTDevice {
pub numerical_id: u64,
pub address: String,
}
impl IoTDevice {
pub fn new(id: u64, address: String) -> IoTDevice {
IoTDevice {
address: address,
numerical_id: id,
}
}
}
#[derive(Debug)]
struct Node {
pub dev: IoTDevice,
left: Tree,
right: Tree,
}
impl Node {
pub fn new(dev: IoTDevice) -> Tree {
Some(Box::new(Node {
dev: dev,
left: None,
right: None,
}))
}
}
// 1. Tree structure itself is only a pointer to the root node
pub struct DeviceRegistry {
root: Tree,
pub length: u64,
}
impl DeviceRegistry {
pub fn new_empty() -> DeviceRegistry {
DeviceRegistry {
root: None,
length: 0,
}
}
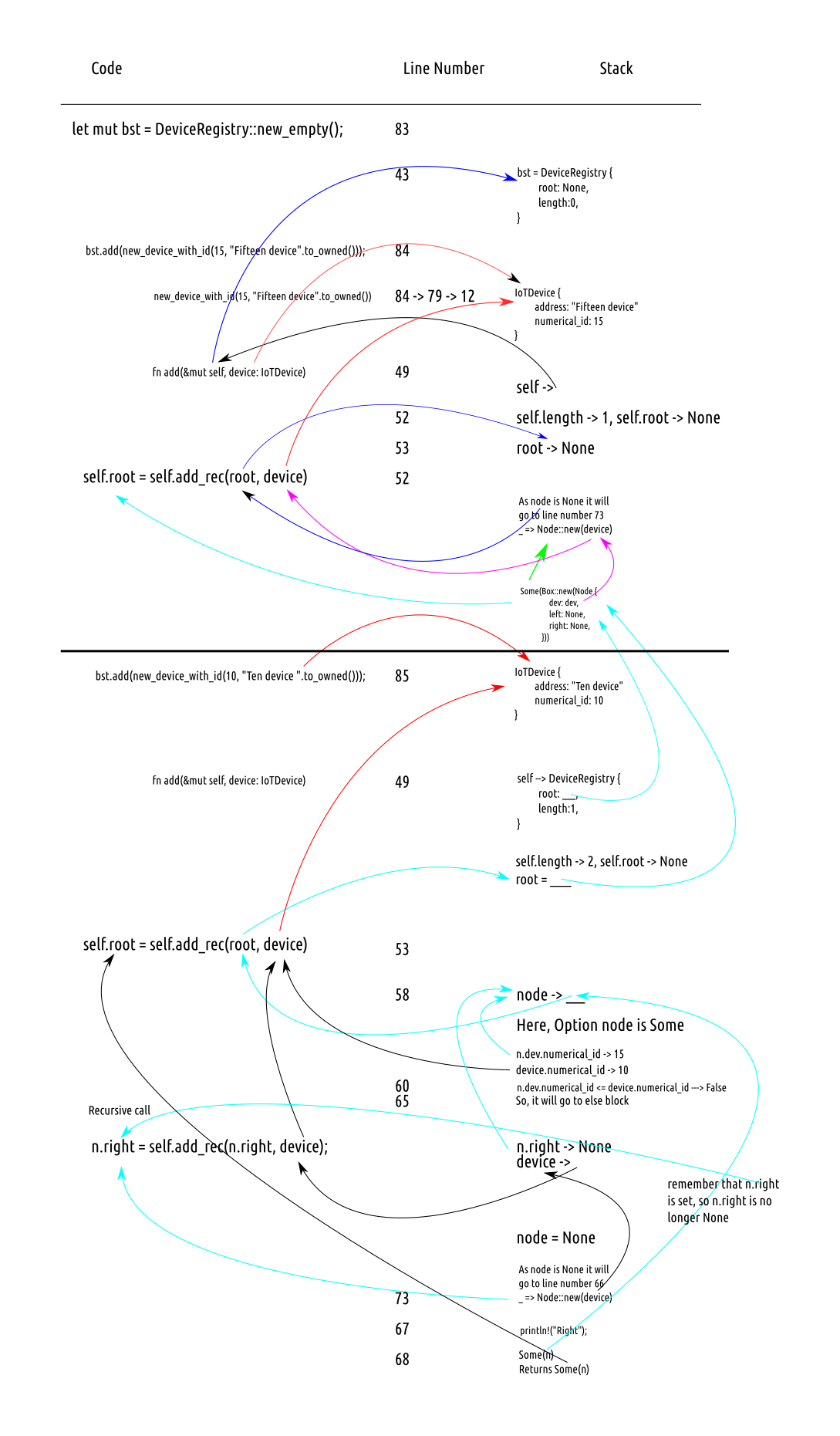
pub fn add(&mut self, device: IoTDevice) {
self.length += 1;
// 2. `self.root` value is given to root, and `self.root` now contains `None`
let root = mem::replace(&mut self.root, None);
self.root = self.add_rec(root, device);
// println!("{:?}", self.root);
}
fn add_rec(&mut self, node: Tree, device: IoTDevice) -> Tree {
match node {
Some(mut n) => {
if n.dev.numerical_id <= device.numerical_id {
n.left = self.add_rec(n.left, device); //recursion
println!("Left");
Some(n)
} else {
n.right = self.add_rec(n.right, device);
println!("Right");
Some(n)
}
}
_ => {
println!("Null node");
Node::new(device)
},
}
}
}
fn new_device_with_id(id: u64, address: String) -> IoTDevice {
IoTDevice::new(id, address)
}
let mut bst = DeviceRegistry::new_empty();
bst.add(new_device_with_id(15, "Fifteen device".to_owned()));
bst.add(new_device_with_id(10, "Ten device".to_owned()));
bst.add(new_device_with_id(20, "Twenty device".to_owned()));
bst.add(new_device_with_id(8, "Eight device".to_owned()));
bst.add(new_device_with_id(12, "Twelve device".to_owned()));
bst.add(new_device_with_id(17, "Seventeen device".to_owned()));
bst.add(new_device_with_id(25, "Twenty Five device".to_owned()));
}
fn main() {
type Tree = Option<Box<Node>>;
#[derive(Clone, Debug)]
pub struct IoTDevice {
pub numerical_id: u64,
pub address: String,
}
impl IoTDevice {
pub fn new(id: u64, address: String) -> IoTDevice {
IoTDevice {
address: address,
numerical_id: id,
}
}
}
#[derive(Debug)]
struct Node {
pub dev: IoTDevice,
left: Tree,
right: Tree,
}
impl Node {
pub fn new(dev: IoTDevice) -> Tree {
Some(Box::new(Node {
dev: dev,
left: None,
right: None,
}))
}
}
// 1. Tree structure itself is only a pointer to the root node
pub struct DeviceRegistry {
root: Tree,
pub length: u64,
}
impl DeviceRegistry {
pub fn new_empty() -> DeviceRegistry {
DeviceRegistry {
root: None,
length: 0,
}
}
pub fn add(&mut self, device: IoTDevice) {
self.length += 1;
// 2. `self.root` value is given to root, and `self.root` now contains `None`
let root = mem::replace(&mut self.root, None);
self.root = self.add_rec(root, device);
// println!("{:?}", self.root);
}
fn add_rec(&mut self, node: Tree, device: IoTDevice) -> Tree {
match node {
Some(mut n) => {
if n.dev.numerical_id <= device.numerical_id {
n.left = self.add_rec(n.left, device); //recursion
println!("Left");
Some(n)
} else {
n.right = self.add_rec(n.right, device);
println!("Right");
Some(n)
}
}
_ => {
println!("Null node");
Node::new(device)
},
}
}
}
fn new_device_with_id(id: u64, address: String) -> IoTDevice {
IoTDevice::new(id, address)
}
let mut bst = DeviceRegistry::new_empty();
bst.add(new_device_with_id(15, "Fifteen device".to_owned()));
bst.add(new_device_with_id(10, "Ten device".to_owned()));
bst.add(new_device_with_id(20, "Twenty device".to_owned()));
bst.add(new_device_with_id(8, "Eight device".to_owned()));
bst.add(new_device_with_id(12, "Twelve device".to_owned()));
bst.add(new_device_with_id(17, "Seventeen device".to_owned()));
bst.add(new_device_with_id(25, "Twenty Five device".to_owned()));
}
Paste the code in the first line of text editor to get the line number.
Some(Node { dev: IoTDevice { numerical_id: 15, address: "Fifteen device" },
left:
Some(Node { dev: IoTDevice { numerical_id: 20, address: "Twenty device" },
left:
Some(Node { dev: IoTDevice { numerical_id: 25, address: "Twenty Five device" },
left: None,
right: None }),
right:
Some(Node { dev: IoTDevice { numerical_id: 17, address: "Seventeen device" },
left: None,
right: None }) }),
right:
Some(Node { dev: IoTDevice { numerical_id: 10, address: "Ten device" },
left:
Some(Node { dev: IoTDevice { numerical_id: 12, address: "Twelve device" },
left: None,
right: None }),
right: Some(Node { dev: IoTDevice { numerical_id: 8, address: "Eight device" },
left: None,
right: None }) }) })
left:
Some(Node { dev: IoTDevice { numerical_id: 20, address: "Twenty device" },
left:
Some(Node { dev: IoTDevice { numerical_id: 25, address: "Twenty Five device" },
left: None,
right: None }),
right:
Some(Node { dev: IoTDevice { numerical_id: 17, address: "Seventeen device" },
left: None,
right: None }) }),
right:
Some(Node { dev: IoTDevice { numerical_id: 10, address: "Ten device" },
left:
Some(Node { dev: IoTDevice { numerical_id: 12, address: "Twelve device" },
left: None,
right: None }),
right: Some(Node { dev: IoTDevice { numerical_id: 8, address: "Eight device" },
left: None,
right: None }) }) })