Graphs
Source:
edX
https://courses.edx.org
PennX: SD3x
Algorithm Design and Analysis
Graphs are represented as set of vertices and a set of edges.
Sometimes they concretely model a network (roads, communication)
but usually represent abstract relationships (people/friendships, documents/similarity)
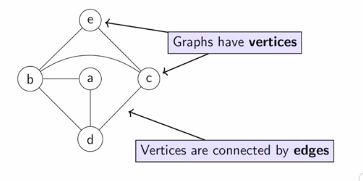
A graph is a finite set of vertices. Here a set of a,b,c,d,e
G = (V, E)
V=> Set of vertices Here, V = {a, b, c, d, e}
E => Set of edges Here, E = {(a,b),(b,e), (a,d),...}
Notice in this graph edges don't have directions. It like a two way street, or communication link where you can send messages in both direction.
Edge (a,b) etc. are unordered pair as it doesn't have direction
Directed Graph: When edges have direction.
Graph Terminology
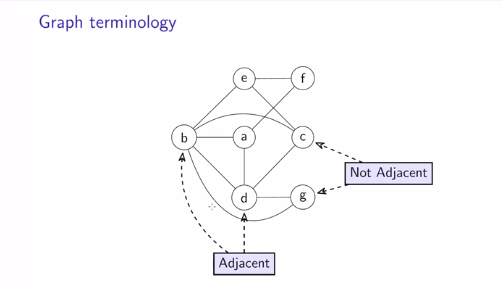
b and g are adjacent, as there is edge between them, and c and g are not adjacent as there is no edge between them.
It doesn't matter how you draw a graph.
Degree of Vertex
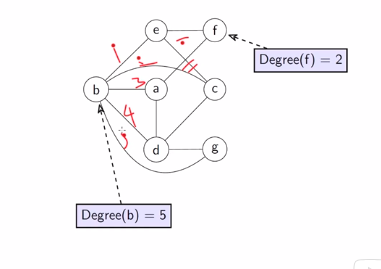
Every vertex has certain number of edges incident on it, the number is called degree
Path
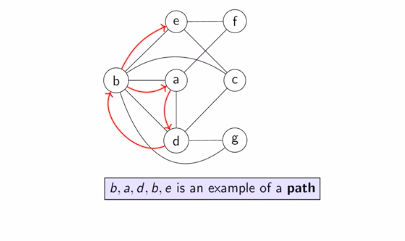
The sequence of vertices, b, a, d, b, e is an example of path
A path is something that you can walk on in the graph.
Notice that vertex b appears twice.
When no vertex appear more than once: Simple path.
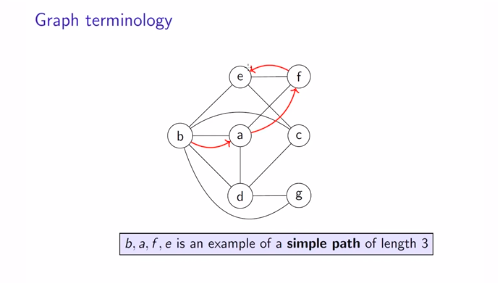
Length of the path: b,a,f,e is 3
Cycles
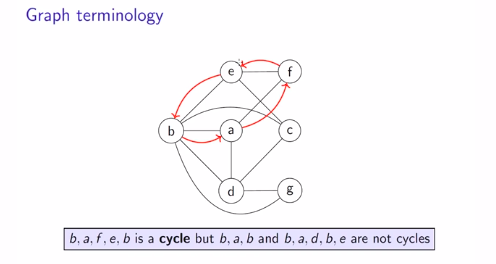
First and last vertex is the same and path should be simple.
Path with length 2 is not a cycle.
We don't allow cycles to repeat vertices except beginning and ending with same vertex.
b,a,d,b,e is not a cycle.
Connected

Graph Types
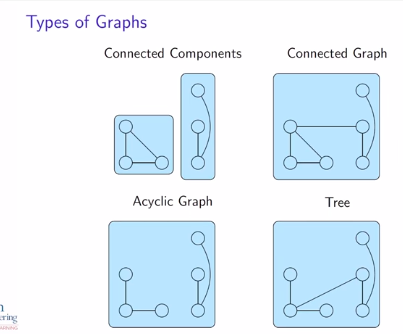
Two vertices in the equivalence relation, if they lie on the same class.
And so the equivalence classes that you get with regard to the connected relation are called connective components of the graph.
Connected Components
In the first diagram, you can see that first three vertices, they form a triangle are all connected to each other so they are in the same equivalence class.
The remaining three vertices are not connected to any of the first three but they are all connected to each other.
So, they form a second equivalence class.
And so, the graph has two connected components.
Connected Graph
A graph with only one connected component like the second figure is called a connected graph.
It's the name given to a graph that has only one connected component.
Meaning you can get from any vertex to any vertex using a path in such a graph
Acyclic Graph
If there are no cycles in it. The third figure.
Tree
A graph is called a tree if it is connected and has no cycles.
And this picture shows that tree, you can see that you can get from any vertex to any other vertex by a path, and there are no cycles. So this is a tree.
What is the relation between the number of vertices and the number of edges in a graph?
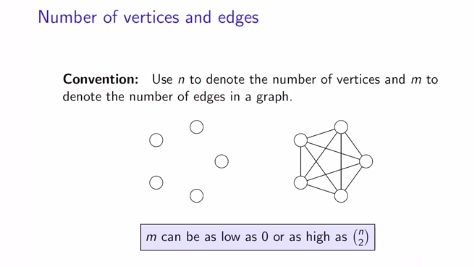
m (edges) can can be as low as 0
m (edges) can be as high as n(vertex) choose 2
Combination:
How many ways there are to choose 2 objects from 5 objects when the order of the objects doesn't matter.
A combination is a group of object that order doesn't matter.
e.g. Soup
Made of chicken, celery and broth
or celery, broth and chicken etc.
Order doesn't matter.
About Tree
In a tree, a vertex of degree 1 is called a leaf.
Theorem: Every tree (with n>=2) has a leaf.
Theorem: A tree T on n vertices has n-1 edges.